La corsa nell'uomo: una visione d'insieme bioenergetica e biomeccanica
di Gian Nicola Bisciotti (1) (2), Sandra Greco (1), Claudio Gaudino(1), Jean Marcel Sagnol(3).

1) Istituto Superiore di Educazione Fisica di Torino (I).
2) Laboratorio di Scienza dello Sport UFR-STAPS, Université de Franche Compté, Besançon (F).
3) Laboratoire Entraînement et Performance UFR-STAPS, Université Claude Bernard, Lyon (F).

Abstract: La corsa, come del resto ogni attività motoria umana, necessita, per una sua giusta comprensione, di una visione d’insieme allo stesso tempo bioenergetica e biomeccanica, questo approccio multidisciplinare può sottolineare degli aspetti fondamentali che, al contrario, possono essere insufficientemente evidenziati quando si adotti una visione monolaterale del problema.

Questo tipo di analisi con le sue conseguenze interpretative può rivelarsi utile, non soltanto nell’ambito della ricerca ma anche, in funzione della razionalizzazione della tecnica, nel campo della metodologia di allenamento.

Introduzione

La corsa, nonostante sia per l’uomo un’attività istintiva e naturale, presenta un’obbiettiva complessità meccanica, in una sua prima analisi, sia pur ridotta e semplificata, possiamo notare come l’energia cinetica (Ecin = _ M · V2) e l’energia potenziale (Epot = m·g ·h) risultino in fase tra loro e come altresì durante la fase di volo nessun tipo di forza esterna, essendo la resistenza dell’aria trascurabile, possa apportare delle modifiche alla bioenergetica del moto stesso.

Inoltre nelle prima parte della fase di volo Epot aumenta a causa della diminuzione dell’ Ecin e diminuisce nella seconda parte quando a sua volta si tramuta in Ecin.

Infine nel momento in cui il piede prende contatto al suolo, si ha una diminuzione dell’energia totale (Etot) del sistema poiché si verifica un abbassamento del centro di gravità simultaneamente alla decelerazione.

Da un punto di vista puramente meccanico quindi la corsa è assimilabile alla successione di rimbalzi di un corpo elastico in cui si possono distinguere una fase aerea effettiva ed un tempo di contatto effettivo.

La meccanica della corsa può quindi essere esemplificata attraverso l’immagine di un pallone che rimbalza al suolo, come è possibile vedere nella Fig. 1.

Nel momento in cui il pallone tocca terra l’Ecin e l’Epot scendono simultaneamente a zero, il pallone risulta infatti fermo per un tempo minimo, in questa fase una parte del lavoro meccanico negativo , imputabile essenzialmente alla deformazione elastica della palla, viene accumulato sotto forma di energia elastica che verrà susseguentemente restituita nel corso del rimbalzo successivo dando luogo in tal modo ad un simultaneo aumento dell’ Ecin e dell’Epot.

Per questo motivo nella corsa, esattamente come nel rimbalzo di un pallone al suolo, non vi può essere alcuna trasformazione di Ecin in Epot e viceversa, tuttavia la fase di accumulo e di conseguente restituzione di energia elastica consente un importante risparmio energetico.

Infine è importante notare come a basse velocità di corsa il rimbalzo del corpo sia sostanzialmente simmetrico, ossia la durata del tempo di contatto effettivo è pari alla durata della fase aerea effettiva, mentre ad alte velocità di corsa tale rimbalzo diviene asimmetrico a causa dell’aumento temporale della fase aerea (Cavagna e coll. 1988 )

La frequenza e l’ampiezza del passo

Il controllo della frequenza e dell’ampiezza del passo sono parametri fondamentali nella valutazione dell’andamento generale della corsa, e costituiscono un aspetto assai importante al fine di ottenere un tipo di corsa il più economico possibile che permetta di realizzare la più alta velocità media in rapporto alla distanza da percorrere. Il concetto di frequenza può essere definito come il numero di movimenti completi compiuti da un punto P nell’unità di tempo (f=1\t), che nel caso specifico della corsa diviene f=1/( T_c+T_v ), dove T_c è il tempo di contatto del piede al suolo e T_v il tempo di volo; tale valore risulta dipendente sia dal numero dei passi che dal tempo considerato.

La velocità di corsa (V) è il risultato del prodotto della lunghezza (SL) e della frequenza del passo (SF), V = SL·SF.

Quando la velocità di corsa aumenta, il soggetto tende ad aumentare la lunghezza della falcata e la sua frequenza di passo, ma mentre SL, pur aumentando in funzione della velocità di corsa, raggiunge un valore stabile ad alte velocità di percorrenza, SF cresce in modo relativamente maggiore a velocità di corsa considerevoli (Williams 1985).

I fattori che determinano questo tipo di adattamento sembrano sostanzialmente incentrati sulla ricerca di una massima economia di corsa basata su di un ottimale frequenza del passo (Dalleau e coll. 1998a,b), questa teoria era già stata avanzata sia da Högberg (1952) è più recentemente da Cavanagh e Williams (1982) che mostrarono come la frequenza spontanea fosse simile alla frequenza che presenta il valore minimo sulla curva del costo metabolico in funzione della frequenza del passo stesso.

Altri Autori hanno suggerito come SF fosse scelta in modo tale da minimizzare, per una data velocità di corsa, la potenza meccanica totale, precisando ulteriormente come in effetti SF abbia effetti opposti sulla potenza meccanica esterna e su quella interna (1), la prima infatti decresce con l’aumentare della frequenza, mentre la seconda al contrario aumenterebbe di valore (Kaneko e coll.1987).

Recentemente Cavagna e coll. (1991) approfondendo la problematica di studio legata agli effetti del cambiamento della frequenza sulla produzione di potenza meccanica, hanno dimostrato come SF spontanea tenda a minimizzare la potenza meccanica prodotta durante un passo effettuato a bassa velocità di corsa, mentre ad elevate velocità di percorrenza tenda a minimizzare unicamente la potenza meccanica della fase propulsiva.

Inoltre è da sottolineare come la stiffness degli arti inferiori, ossia la loro rigidità muscolo-tendinea, aumenti linearmente in funzione della frequenza dei passi (Farley e Gonzales 1996) provocando in tal modo un aumento della trasmissione degli shocks generati dall’impatto del piede al suolo (Mc Mahon 1984, Mc Mahon e coll. 1987, Lafortune e coll. 1996).

In seguito affronteremo la tematica inerente a come, durante la corsa, il soggetto cerchi di adattare la frequenza del passo sia in funzione di un’ottimale economia di corsa che di una minimizzazione degli shocks trasmessi all’apparato osteo-muscolo-legamentoso.

Anche la lunghezza del passo riveste un ruolo determinate nel dispendio energetico e nel rendimento della corsa, infatti il VO2 per un data velocità di corsa aumenta in maniera curvilinea rispetto all’aumento od alla diminuzione della lunghezza del passo naturalmente scelta dall’atleta (Höeberg 1952, Cavanagh e Williams 1982), recenti studi hanno inoltre dimostrato come attraverso la correzione effettuata tramite retrocontrollo audiovisuale di una lunghezza di passo non ottimale (ossia non corrispondente ad una minimo consumo di O2 ) si sia potuta ottenere una diminuzione della richiesta energetica della corsa stessa (Morgan e coll. 1994).

Rendimento e costo energetico della corsa

Il rendimento muscolare in situazioni di attivazione naturale risulta essere di circa il 25% (Cavagna e coll. 1964), tuttavia nella corsa il rendimento raggiunge percentuali di circa 40-50%, mentre in altre attività muscolari come il ciclismo questa percentuale raggiunge solamente circa il 20% (Gaesser e Brooks,1975)

Questo aumentato rendimento muscolare nel caso della corsa sembra essere attribuibile alla restituzione di energia elastica che avviene durante la biomeccanica della corsa stessa.

Nella fase eccentrica infatti viene accumulata energia elastica nella componente elastica seriale (essenzialmente il tendine e la parte S2 della miosina) della muscolatura che viene sottoposta ad allungamento, energia che viene poi restituita sotto forma di lavoro meccanico potenziando la successiva fase concentrica.

Il recupero dell’energia elastica immagazzinata nella fase eccentrica permetterebbe quindi una diminuzione della spesa energetica (Cavagna e coll. 1964, Cavagna e coll. 1968, Shorten 1987) inoltre il ruolo svolto dal recupero di energia elastica sarebbe ancor più rilevante a velocità di corsa elevate (Bosco e Rusko 1983).

Il fenomeno di stoccaggio e restituzione di energia elastica è stato confermato sperimentalmente da misurazioni effettuate con l’ausilio della piattaforma di forza, dove è riscontrabile come la forza di reazione al suolo sia una funzione lineare dello spostamento del corpo (Cavagna e coll.1988) ed è proprio questa linearità che suggerisce come il comportamento dell’arto di appoggio sia simile a quello di una molla, concetto che descriveremo successivamente in modo più specifico nello Spring Mass Model (Alexander 1988) .

Il costo energetico della corsa (C_r), si ottiene dividendo il VO₂ netto, corrispondente ad una velocità sottomassimale determinata, per la velocità stessa (Margaria, 1938;Margaria e coll.,1963) :

C_r = (VO₂ - VO_{2 riposo}) · v^-1

Dove V O₂ è espresso in ml · kg ·s^-1 e v è la velocità di corsa espressa in m · s^-1, in tal modo C_r risulta essere espresso in ml di O₂ oppure in Joules per kg di massa corporea e per metro percorso.

Tale valore rimane comunque legato a delle costanti individuali molto specifiche, tuttavia il C_r si rivela indipendente rispetto alla velocità di corsa sino a valori di circa 6 m · s^-1 (Åstrand, 1952; Krahenbuhl e coll,1979; Conley e Krahenbuhl, 1980; Davies, 1980; Brandsford e Howley, 1977; Di Prampero e coll., 1986 e 1993) e risulta essere di circa 0.9 kcal · kg^-1 · km^-1 per tale motivo è possibile paragonare il C_r interindividuale a diverse velocità di percorrenza .

Tuttavia questo tipo di calcolo del dispendio energetico risulta affidabile soltanto nel caso di velocità di percorrenza costante, in altre parole il dispendio energetico della corsa risulta essere di questo tipo solamente in caso di assenza di fasi rilevanti di accelerazione e decelerazione.

Infatti, ipotizzando che il costo dell’accelerazione sia uguale a _ M V² _max ( dove M è la massa dell’atleta e V _max la velocità massima raggiunta ) ( Di Prampero 1985) ed il rendimento muscolare pari a circa il 25% ( Cavagna 1988 ) è possibile calcolare indirettamente il costo energetico supplementare relativo alle fasi di accelerazione eventualmente presenti nella corsa stessa.

L’esempio seguente potrà chiarire maggiormente il concetto sovraesposto:

Supponendo che un atleta corra reiteratamente un tratto di 20 m.t. a velocità sub-massimale (compresa tra 2 e 4 m.t · s-1 ) in corsa-navette, ovverosia invertendo la direzione di corsa ogni 20 m.t. di percorrenza attraverso un cambio di direzione seguito da una fase di accelerazione stimata di una lunghezza di circa 2.5 m.t., il rapporto tra la sua velocità massimale (Vmax) e la sua velocità media (Vmed) può essere calcolato come segue:

Vmed = (2.5 Vmax)/2 + 15 Vmax + (2.5 Vmax)/2

20

da cui : Vmax = 8/7 Vmed

Con lo stesso tipo di calcolo è possibile stimare il rapporto tra Vmax e Vmed se la stessa quantità totale di corsa viene effettuata a parità di tempo ma invertendo la direzione di corsa ogni 10 m.t. (navette 10 m.t.) od ogni 5 m.t. (navette 5 m.t.) ossia rispettivamente raddoppiando e quadruplicando i cambi di direzione e conseguentemente le fasi di accelerazione :

Nel caso di due tratti da 10 m.t. avremo:

Vmed = (2.5 Vmax)/2 + 5 Vmax + (2.5 Vmax)/2

10

da cui: Vmax = 4/3 Vmed

Nel caso invece di quattro tratti da 5 m.t. il calcolo sarà il seguente:

Vmed = (2.5 Vmax)/2 + (2.5 Vmax)/2

5

da cui: Vmax = 2 Vmed

Nel caso di una corsa-navette prolungata con cambio di direzione ogni 20 m.t. l’energia cinetica (Ecin) richiesta per le fasi di accelerazione sarà dunque pari a :

Ecin = _ M V2 = _ M (2 Vmed) 2

Da cui:

Ecin = _ M (8\7 Vmed ) 2 = 64/98 M V2 med » 0.65 M V2 med

Nel caso di una corsa-navette prolungata con cambio di direzione ogni 10 m.t. l’energia cinetica (Ecin) richiesta per le fasi di accelerazione sarà pari a :

Ecin = _ M V2 = _ M (2 Vmed) 2

Da cui:

Ecin = _ M (4/3 Vmed ) 2 = 16/18 M V2 med » 0.89 M V2 med

Infine nel caso di una corsa-navette prolungata con cambio di direzione ogni 5 m.t. l’energia cinetica (Ecin) richiesta per le fasi di accelerazione sarà pari a :

Ecin = _ M V2 = _ M (2 Vmed) 2

Da cui :

Ecin = 4/2 M V2 med = 2 M V2 med

Riepilogando quindi nella corsa-navetta prolungata con cambio di direzione ogni 20 m.t., Vmax sarà uguale a 8/7 Vmed e l’Ecin = 64/98 MV2 med.

Nel caso di una corsa-navetta prolungata con cambio di direzione ogni 10 m.t., Vmax sarà uguale a:

4/3 Vmed ed Ecin = 16/18 MV2 med.

Infine nel caso di una corsa-navetta prolungata con cambio di direzione ogni 5 m.t., Vmax sarà uguale a 2 Vmed ed Ecin = 2 MV2 med.

Assumendo che il costo metabolico della corsa nell’uomo sia pari a circa 0.9 Kcal · kg-1 · km, e trasformando il costo metabolico della presente in Joule (essendo 1 Kcal pari a 4,18 kJ ), avremo un costo energetico per metro pari a circa :

4 J · M

nella quale M è la massa del soggetto espressa in kg.

Da cui potremmo calcolare che il costo energetico sui diversi tipi di frazionamento di corsa-navetta:

corsa frazionata su tratti di 5 m.t. : J » 20 · M

corsa frazionata su tratti di 10 m.t. : J » 40 · M

corsa frazionata su tratti di 20 m.t. : J » 80 · M

Ipotizzando ad esempio una velocità di percorrenza media pari a 2 m.t. · sec —1 ed un rendimento muscolare pari al 25%, il costo energetico necessario alle fasi di accelerazione di una corsa-navetta frazionata in tratti da 5 m.t. sarà pari a:

Ecin = 2 M · (2)2 / 0.25 =32 M

Nel caso di una corsa-navetta frazionata in tratti da 10 m.t. il costo energetico inerente alle fasi di accelerazione sarà pari a:

Ecin = 16/18 M · (2)2 / 0.25 = 14,22 M

Infine nel caso di una corsa-navetta frazionata in tratti da 20 m.t. il costo energetico inerente alle fasi di accelerazione sarà pari a:

Ecin = 64/98 M · (2)2 / 0.25 = 10.45 M

Per cui il costo totale (Etot) di una corsa prolungata frazionata in tratti-navetta di 5 m.t. percorsi ad una Vmed di 2 m.t. · s-1 sarà pari a :

Etot = 10 M +32 M = 42 M

per cui ogni tratto totale di 20 m.t. comporterà un dispendio totale di 168 J ·kg-1

Nel caso di tratti-navetta di 10 m.t. sarà pari invece a :

Etot = 30 M + 14.22 M = 44.22 M

per cui ogni tratto totale di 20 m.t. comporterà un dispendio totale di 88,44 J ·kg-1

Infine nel caso di corsa-navetta frazionata in tratti di 20 m.t. si avrà un costo pari a :

Etot = 70 M + 10,45 M = 80,45 J ·kg-1 per ogni tratto considerato.

Nel caso dello stesso tipo di percorrenza effettuato però ad una velocità doppia (4 m.t. · sec-1) rispetto all’esempio precedente, Etot sarà pari a:

Etot 5 m.t. = 10 M + 128 M = 138 M

rapportato ad un tratto di 20 m.t. quindi

Etot = 552 J ·kg-1

Etot 10 m.t. = 30 M + 57 M = 87 M

Rapportato ad un tratto di 20 m.t. quindi

Etot = 174 J ·kg-1

Etot 20 m.t. = 70 M + 42 M = 112 J ·kg-1

Il dispendio energetico della corsa quindi sarebbe fortemente correlato al numero delle fasi di accelerazione ed alla velocità media da mantenersi in funzione delle accelerazioni stesse nonché al cambio di frequenza di passo che tali fasi di accelerazione e decelerazione comportano, come vedremo più avanti infatti l’adozione di una frequenza di passo che si allontani dalla frequenza naturale, comporta un maggior dispendio energetico.

Infatti dai calcoli sopraindicati possiamo desumere come alla Vmed di 2 m.t. sec-1 il costo metabolico di un tratto di corsa di 20 m.t. salga di circa 1,1 volte quando lo stesso tratto venga percorso in due tratti navette di 10 m.t. e di circa 2 volte nel caso in cui venga percorso in quattro tratti navette di 5 m.t.

Questi costi salgono ulteriormente a 1.5 ed a 4,9 nel caso di percorrenza alla Vmed di 4 m.t. sec-1 .

Questi calcoli teorici possono essere ritenuti sufficientemente coerenti ai dati registrati nel corso di una sperimentazione nella quale a 14 giocatori di calcio di medio livello di età pari a 25 +4 anni veniva richiesto di effettuare una corsa -navetta sino ad esaurimento su tratti di 20, 10 e 5 m.t. a velocità progressivamente crescenti ( comprese tra 2.5 e 3.6 m.t. sec-1 ) secondo il protocollo di test di Léger e coll. (Leger e coll. 1982a, 1982b,1984,1985).

I risultati registrati indicano un decremento della durata e della velocità massima di percorrenza pari al 41.01+6.42% tra navette 20 m.t. e navette 10 m.t., del 73.74+5.31% tra navette 20 m.t. e navette 5 m.t. e del 54.73+11.47% nel caso di navette 10 m.t. e navette 5 m.t. (Bisciotti, Belli 1998).

Tali risultati, anche se richiedono un ulteriore approfondimento sperimentale attraverso un protocollo che preveda la misurazione diretta del consumo di O2, rendono evidente la difficoltà nella quantificazione del dispendio energetico in alcune attività come il calcio, il rugby, la pallacanestro od il tennis, nelle quali la corsa è caratterizzata dall’alternarsi di fasi di accelerazione a fasi corsa blanda a velocità pressoché costante ed a continui cambi nella frequenza del passo di corsa dettati dall’esigenza di essere in sintonia con la traiettoria e la velocità della palla.

Da quanto esposto appare quindi chiara la necessità dell’appropriata metodologia di allenamento che tali attività richiedano proprio in virtù della loro specificità bioenergetica.

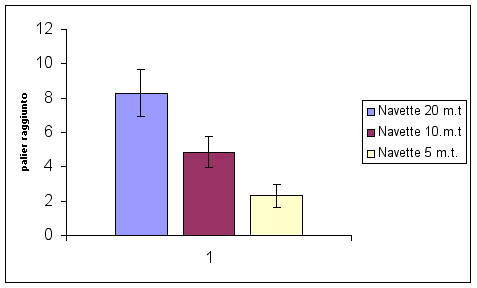
Palier raggiunto in funzione dell’aumento dei cambi di direzione e delle conseguenti fasi di accelerazione di 3 differenti modalità di corsa - navetta (20,10 e 5 m.t.).

Ogni palier corrisponde ad 1’ di corsa a velocità progressivamente crescente, per cui maggiore è il palier raggiunto maggiore risulta essere la più alta Vmed di percorrenza registrata durante il test (Bisciotti, Belli 1998).

Il rapporto tra VO2 e Cr

Il VO_{2 max} espresso in ml·kg^-1 è sempre stato considerato uno dei parametri maggiormente discriminanti nell’ambito della performance della corsa prolungata (Saltin e Åstrand , 1967; Costil e coll., 1973 ; Boileau e coll., 1982).

Il C_r rimane tuttavia correlato negativamente rispetto al peso e all’altezza individuale, dal momento che questi due fattori sono difficilmente discriminabili per poter valutare coerentemente il VO_{2 max} indipendentemente dalla massa, occorrerebbe dare a quest’ultima un esponente uguale a 0,75 (Svendenhag e Sjödin, 1994) apparirebbe più corretto quindi legare il concetto di rendimento di corsa a quello di VO₂ ·ml^-1·kg^-0.75 , in tal modo il VO₂ (lt · min^-1) sarebbe proporzionale alla massa potenza di 2/3.

Tuttavia il VO₂ max non è il solo elemento esplicativo nelle differenze interindividuali del rendimento della bioenergetica della corsa, in effetti il fattore maggiormente discriminante nei confronti della massima velocità di corsa sostenibile sembrerebbe essere attribuibile al C_r .

In effetti un miglioramento del 10% del C_r comporterebbe un aumento del 12% della Velocità Aerobica Massimale (Va _max, ) che a sua volta consentirebbe un aumento nella velocità massimale di corsa pari al 9% nel corso di una prestazione di 5.000 m.t. (Lacour, 1990).

La Va _max, concetto introdotto da Di Prampero nel 1986, è ottenibile attraverso l’applicazione della seguente formula :

Va _max = (VO_{2 max} - 0.083) · C_r^-1

Dove VO₂ è espresso in ml · kg-1 · s-1, v in m · s-1 ed il valore di 0.083 ml · kg -1· s-1 ( 5 ml · kg-1 · m-1 ), stabilito da Medbø e coll (1988), è la media dell’intercettazione dell’asse y nella relazione lineare VO₂ · v-1ottenuta durante la corsa su treadmill e corrisponde al VO₂ a riposo dell’atleta in piedi sul treadmill stesso.

Dal momento che le possibilità di aumento del Cr nella bioenergetica individuale di corsa sono comprese in un range che va dal 5 al 16% del C_r totale (Conley e coll., 1981 e Conley e coll., 1984), è importante ricordare l’importanza che riveste il C_r nell’economia totale di corsa.

Lo Spring Mass Model

Come già precedentemente ricordato, nella biomeccanica e nella bioenergetica della corsa l’elasticità muscolare svolge un ruolo molto importante, per questo motivo nell’ambito della modellizzazione della corsa sia nell’uomo che in alcuni tipi di animali, come ad esempio il canguro od il montone, si è arrivati alla concettualizzazione di un modello meccanico costituito da una massa , che riveste il ruolo della massa corporea totale in serie ad una componente elastica , sotto forma di una molla, che modellizza gli arti inferiori e le loro caratteristiche elastiche.

Nell’interpretazione concettuale di tale modello un elemento esplicativo della variazione interindividuale del C_r nella bioenergetica della corsa umana, può essere attribuito alla stiffness neuromuscolare.

La stiffness neuromuscolare è definibile come una variazione di forza su una variazione di lunghezza ed è quantificabile matematicamente come il rapporto di D F/D L nel quale D L è una funzione lineare della forza D F (Cavagna,1988).

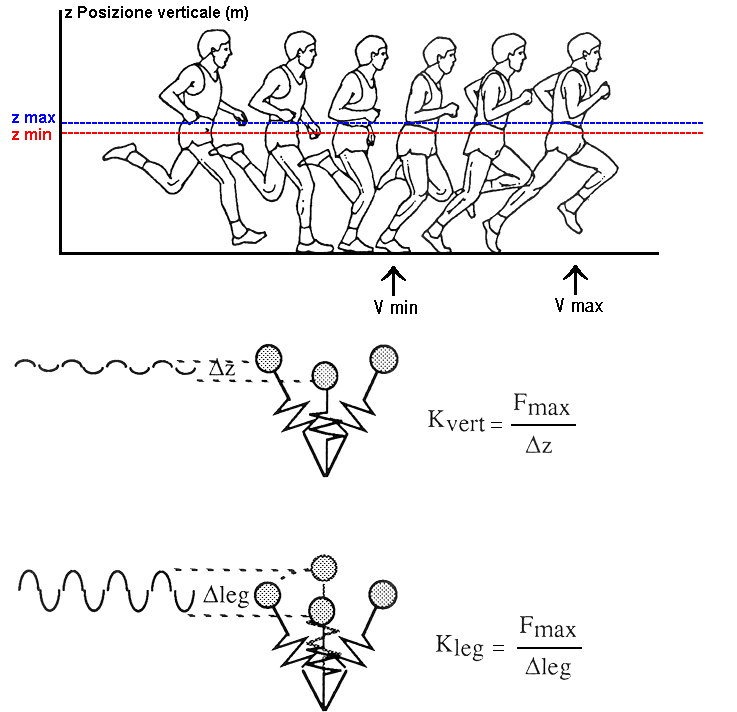
Figura 1: lo Spring Mass Model applicato alla biomeccanica della corsa (Mc Mahon e Cheng, 1990). In questo tipo di modello, se si osservano solamente le oscillazioni sul piano verticale del corridore, si parla di stiffness verticale (K_vert), mentre se si tiene conto del reale accorciamento della gamba si parla di stiffness dell’arto inferiore (K_leg)

Lo Spring Mass Model (Alexander e Vernon, 1975) inizialmente concepito per lo studio del meccanismo di stoccaggio e restituzione di energia elastica nella locomozione del canguro, è stato applicato con successo anche nell’ambito della locomozione umana (Alexander, 1988; Blickhan, 1989;Mc Mahon, 1990;Mc Mahon e Cheng, 1990).

Quando questo tipo di modellizzazione viene applicato alla corsa nell’uomo, occorre distinguere tra K_vert e K_leg ( Mc Mahon e Cheng 1990 ), intendendo per K_vert le oscillazioni verticali del corridore, e riferendosi in questo caso alla stiffness verticale, e per K_leg il reale accorciamento dell’arto inferiore d’appoggio, intendendo in tal caso la stiffness degli arti inferiori.

Per meglio comprendere il concetto di stiffness occorre fare riferimento alla "rigidità" della struttura meccanica considerata, che nel caso specifico è la struttura muscolo- tendinea.

Ogni struttura meccanica quando subisce una perturbazione della sua posizione di equilibrio, vibra ad una frequenza variabile che dipende dalla sua massa e dal suo valore di stiffness K.

La frequenza di risonanza si può calcolare applicando la seguente equazione che definisce la frequenza di un moto armonico:

RF = 1/ 2p Ö K/M

Dove K è la rigidità ed M la massa del corpo.

Il valore di rigidità K può essere quantificato attraverso differenti tipi di calcolo, il metodo più classico può forse essere considerato quello di Farley e coll. ( 1991) che, assimilando il soggetto ad un sistema composto appunto da una massa e da una molla rimbalzante al suolo , parte dal presupposto concettuale che la forza esercitata da tale complesso sul suolo stesso passi per il suo peso durante il periodo di contatto e di stacco. La durata tra questi due istanti, misurata su pedana di forza, è considerata come la metà del periodo di risonanza del sistema oscillante (T/2) , e la rigidità del sistema massa-molla rimbalzante al suolo e quindi calcolata attraverso la formula :

K = p 2 / (T/ 2) 2 (in N · m-1 · kg-1)

In tal modo conoscendo la frequenza reale del passo (SF), si può calcolare la differenza relativa D F % risultante dal rapporto tra SF e RF applicando la seguente formula:

D F % = (SF — RF)· RF^-1 %.

Un primo dato interessante che occorre sottolineare è come il C_r risulti inversamente correlato alla rigidità e direttamente correlato alla differenza tra SF ed RF, ossia maggiore risulti questa differenza, maggiore appare essere il costo energetico della corsa stessa (Dalleau e coll. 1998a,b).

Sembrerebbe quindi che la frequenza ideale di passo alla quale il C_r è minimo, sia prossima alla frequenza naturale di oscillazione del sistema (Cavagna e Franzetti 1982, Kaneko e coll. 1987)

In effetti quando un sistema formato da una massa ed un corpo elastico, come nel caso dello spring mass model, viene forzato ad una frequenza RF, la forza e l’energia necessaria per realizzare una data ampiezza di movimento sono minime, in altri termini RF è la frequenza che permette il mantenimento di un movimento oscillante ad una data ampiezza con un dispendio energetico minimo, per questo motivo numerosi autori indicano come RF possa minimizzare il dispendio energetico anche nel movimento umano (Mc Mahon 1984, Taylor 1985, Dalleau e coll. 1998a,b).

E’ comunque interessante notare che il valore minimo di C_r non corrisponda al valore massimo di rendimento, infatti nel momento in cui la frequenza aumenta si verifica un aumento del C_r stesso probabilmente dovuto ad un parallelo aumento del costo meccanico ( Kaneko 1990 ).

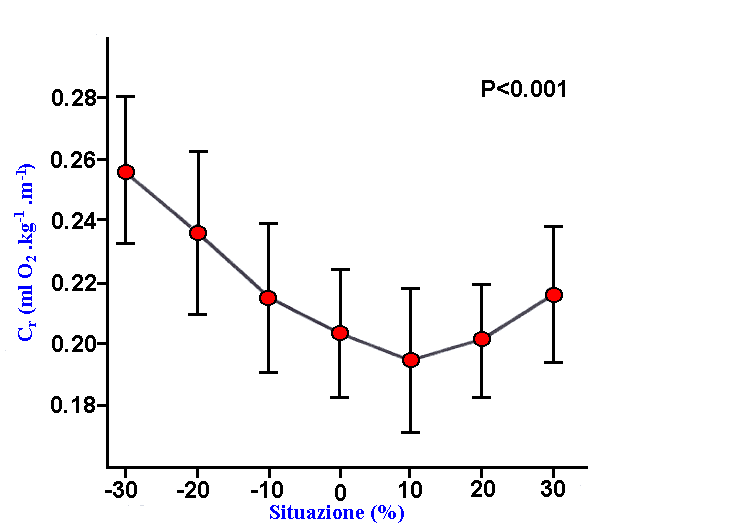
Figura 2: influenza della variazione della frequenza dei passi sul Cr ( da Dalleau e coll. 1998a, modificato).

Infatti dal momento che la stiffness degli arti inferiori risulta essere una funzione lineare della frequenza dei passi (Farley e Gonzales, 1996 ) ad elevate frequenze di passo interverrebbe probabilmente un aumento della stiffness del sistema neuro-muscolare con un conseguente maggior lavoro meccanico interno (Dalleau, 1998a), inoltre occorre ricordare come una stiffness elevata comporterebbe un aumento dello shock trasmesso al sistema muscolo-scheletrico, favorendo probabilmente l’insorgenza di lesioni a carico dell’apparato locomotore (McMahon 1984, McMahon e coll. 1987).

Numerosi sono infatti gli studi che confermano l’aumento dei valori di stiffness in rapporto all’aumento della velocità di percorrenza, Blickhan (1989) riferisce valori di stiffness che variano entro i 10 kN · m-1 a 3 m · s -1 e 30 kN · m-1a 9 m·s—1, Farley e Gonzales (1996) riportano valori di stiffness dell’ordine di 11 kN· m-1 alla velocità di 2.5 m · s-1, mentre Viale e coll. (1997) riferiscono valori di 13 kN · m-1 ad una velocità di percorrenza pari a 4 m · s-1 . infine Dalleau e coll. (1998a,b) riferiscono come la stiffness neuro-muscolare raddoppi di valore nel momento in cui la frequenza passi dal —30% al +30% della frequenza di passo spontanea, indicando in tal modo come la stiffness possa dipendere non solo dall’aumento della velocità di percorrenza ma anche dalla frequenza.

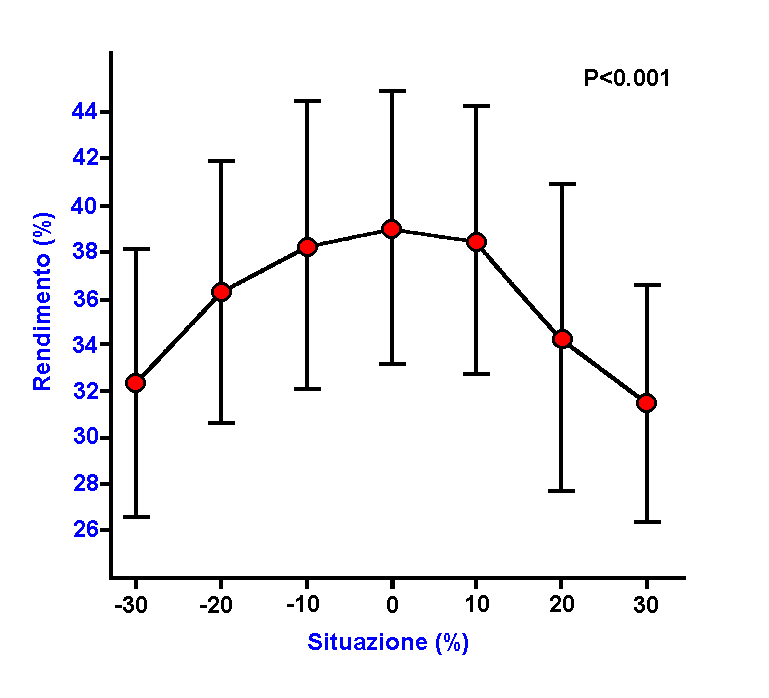
Figura 3: Influenza della variazione della frequenza dei passi sul rendimento ( da Dalleau e coll. 1998a, modificato.

Inoltre dal momento che la stiffness degli arti inferiori è riconducibile sia alla rigidità muscolo-tendinea dei muscoli estensori della gamba sia alla struttura elastica del piede (Kerr e coll.1987, Alexander 1988, Alexander 1997), è interessante notare come un piede supinato sia maggiormente rigido di un piede pronato e come questo comporti un irrigidimento del sistema durante la corsa (Viale e coll.1998)

E’ importante infine ricordare che la stiffness, anche se risulta fortemente influenzata sia dalla rigidità dei ponti acto-miosinici che da quella dei tendini (Shorten 1987, Alexander 1988), è modulabile solo attraverso l’attivazione neuro-muscolare.

Da quanto sopra esposto quindi sembra che durante la corsa il massimo rendimento si abbia quando il soggetto possa modulare la rigidità del suo apparato muscolo-tendineo in maniera tale che RF del modello sia il più simile possibile ad SF reale.

Tuttavia SF tende ad identificarsi con RF soprattutto a basse velocità di corsa (Cavagna e coll. 1988) mentre per velocità più elevate, alle quali interverrebbe un aumento della stiffness con conseguente maggior shock a carico dell’apparato locomotore, il soggetto tende ad adottare una frequenza del 10% inferiore, in tal modo sembra che l’atleta preferisca una frequenza di corsa inferiore con un conseguente maggiore Cr, visto che quest’ultimo presenterebbe il suo valore minimo ad un valore di frequenza superiore del 10% rispetto alla frequenza spontanea, probabilmente al fine di ottimizzare il compromesso tra la necessità di preservare le proprie strutture anatomiche e la massimalizzazione della performance legata al minimo dispendio energetico (Dalleau e coll. 1988a,b).

Alla luce di queste considerazioni possiamo avanzare l’ipotesi che la regolazione della stiffness dell’apparato muscolo-tendineo durante la corsa, attuabile attraverso una regolazione neuro-muscolare, possa essere interpretabile anche come un meccanismo di protezione contro i microtraumatismi ripetuti dovuti allo shock dell’impatto del piede al suolo.

Un ulteriore dato interessante che può emergere da un’analisi approfondita di questo tipo di modellizazione muscolare è che calcolando la rigidità, la frequenza di risonanza ed il lavoro meccanico di ogni arto separatamente, possiamo constatare come un arto rispetto al controlaterale realizzi una maggior quantità di lavoro meccanico e possa essere per questa ragione definito "arto propulsivo" dal momento che risulta essere quello che svolge l’azione propulsiva orizzontale e verticale maggiore, mentre l’altro è definibile come arto di appoggio, vista la sua minore azione di flessione-estensione durante la fase di supporto (Cavanagh 1990), questa asimmetria nella produzione di lavoro positivo è quantificabile in circa il 20% (Dalleau e coll. 1998a,b).

Conclusioni

L’ottimizzazione dei vari parametri che costituiscono quella che per l’uomo risulta essere una delle attività più istintive e naturali quali la corsa comporta, nel momento in cui la performance venga estremizzata come nella realtà sportiva di alto livello, una profonda conoscenza di tutti i suoi aspetti biomeccanici ed energetici.

Per questo motivo non solo sarebbe auspicabile una profonda conoscenza teorica di questi ultimi anche da parte del tecnico sportivo ma ancor di più risulterebbe fondamentale una stretta collaborazione tra il ricercatore e l’ "uomo di campo" allo scopo di individuare su solide basi scientifiche le migliori metodologie di allenamento atte al miglioramento della prestazione onde evitare l’applicazione di una linea metodologica di lavoro basata su quel tanto sino ad oggi utilizzato metodo di apprendimento" per prove ed errori" che nasce da un sostanziale empirismo valutativo e che non ha più ragione di esistere nell’ambito della prestazione sportiva di alto profilo qualitativo.

Nota: (1) Per potenza meccanica esterna si intende la potenza relativa agli spostamenti del centro di gravità del corpo rispetto al suolo e per potenza meccanica interna quella relativa allo spostamento degli arti rispetto al centro di gravità.

Bibliografia

Alexander R.M. (1988) Elastic mechanism in animal movement. Cambridge University Press. Cambridge.

Alexander R.M. (1997) Invited editorial on "interaction of leg stiffness and surface stiffness during human hopping". J. Appl. Physiol. 82: 13-47.

Alexander R.M., Vernon A. (1975) The mechanics of hopping by kangaroos (Macropodidae). Journal of Zoologie, London 177: 265-303.

Åstrand P.O. (1952) Experimental studies of physical working capacity in relation to sex and age. Munsksgaard Copenhagen.

Bisciotti G.N., Belli A. (1998) dati non pubblicati.

Blickhan R. (1989) The spring-mass model for running and hopping. J Biomechanics 22: 1217-1227

Bolieau R.A., Mayhew J.L., Riner W.F., Lussier L. (1982) Physiological characteristics of elite middle and long distance runners. Can. J. Appl. Sport. Sci. 7: 167-172.

Bosco C., Rusko H. (1983) The effect of prolonged skeletal muscle stretch-shortening cycle on recoil of elastic energy and on energy expenditure. Acta Physiol. Scand. 119 : 219-224

Bransford D.R., Howley E.T. (1977) Oxygen cost of running in trained and untrained men and women. Med. Sci. Sports. 9 : 41-44.

Cavagna G. A., Franzetti P. (1982) Step frequency in walking. IRCS Medical Science 10: 281-282

Cavagna G.A. (1988) Muscolo e locomozione. Raffaello Cortina Editore. Milano

Cavagna G.A., Dusman B., Margaria R. (1968) Positive work done by a previously streched muscle. J. Appl. Physiol.. 24 : 21-32.

Cavagna G.A., Franzetti P., Heglund N.C., Willems P. (1988) The determinants frequency in running, trotting an hopping in man and other vertebrates . J. Physiol. (London) 399: 81-92

Cavagna G.A., Saibene F.P., Margaria R. (1964) Mechanical work in running. J. Appl. Physiol.. 19 : 249-256.

Cavagna G.A., Willems P.A., Franzetti P., Detrembleur C. (1991) The two power limits conditionning step frequency in human running . Journal of Physiology 437 : 95-108.

Cavanagh P.R (1990). Biomechanics: a bridge builder among the sport sciences . Med. Sci. Sports. Exerc. 17: 304-308.

Cavanagh P.R., Williams K.R. (1982) The effect of stride length variation on oxygen uptake during distance running. Med Sci Sport Exerc 14 : 30-35.

Coneley D., Krahenbuhl G., Burkett L. (1981) Training for aerobic capacity and running economy. Physician and Sportsmed. 9: 107-115.

Coneley D., Krahenbuhl G., Burkett L., Milar L. (1984) Following Steve Scott: physiological changes accompanying training.Physician and Sportsmed. 12: 103-106.

Conley D., Krahenbuhl G.S. (1980) Runnig economy and distance running performance of highly trained athletes. Med. Sci. Sport Exerc. 12 : 357-360.

Costill D.L., Thomason H., Roberts E. (1973) Fractional utilization of the aerobic capacity during distance running. Med. Sci. Sports. 5 : 248-252.

Dalleau G. (1998a) Influence du contrôle de la raideur musculo — tendineuse lors de la locomotion. Apport de nouvelles méthodes de mesure. Thèse de Doctorat, Université Claude Bernard Lyon I.

Dalleau G., Belli M., Bourdin M., Lacour J. R., (1998b) The spring — mass model and the energy cost of treadmill running. European Journal of Applied Physiology. In corso di pubblicazione.

Davies C.T.M. (1980) Metabolic cost of exercice and physical parformance in children with some observation on external loading. Eur. J. Appl. Physiol. 39 : 249-254.

Di Prampero P.E. (1985) La locomozione umana su terra, in acqua in aria. Fatti e teorie. Edi. Ermes Milano

Di Prampero P.E. (1986) The energy cost of human locomotion on land and in water. Int. J. Sports Med. 7 : 55-72.

Di Prampero P.E., Cappelli C., Pagliaro P., Antonutto G., Girardis M., Zamparo p., Soule R.G. (1993) Energetics of best performances in middle-distance running. J. Appl. Physiol. 74: 2318-2324.

Farley C.T., Gonzales O. (1996) Leg stiffness and stride frequency in human running . J Biomechanics. 29 : 181-186.

Gaesser G.A., Brooks G.A. (1975) Muscular efficiency durin steady-state exercice : effect of spedd and work rat. J. Apll. Physiol . 38 : 1132-1139.

Höeberg P. (1952) Length of stride, stride frequency, flight period and maximum distance between the feet during running with different speeds. Arbeit Physiologie. 14: 431-436.

Kaneko M. (1990) Mechanics and energetics in running with reference to efficiency. J. Biomechanics 23: 57-63.

Kaneko M., Matsumoto M., Ito A., Fuchimoto T (1987) Optimum step frequency in constant speed running. Biomechanics X-B : 803-805.

Kerr R.F., Bennet M.B., Bibby S.R., Kester R.C., Alexander R.M. (1987) The spring in the arch of the human foot. Nature 325: 147-149.

Krahenbuhl G.S., Pangrazi R.P., Chomokos E.A. (1979) Aerobis reponses of young boys to submaximal running. Res. Quart. 50 (3) : 413-421.

Lacour J.R., Padilla-Magunacelaya S., Barthelemy J.C., Dormois D. (1990) The energetics of middle-distance running. Eur. J. Appl. Physiol. 60: 38-43.

Lafortune M.A., Henning E.M, Lake M.J. (1996) Dominant role of interface over knee angle for cushioning impact loading and regulating initial stiffness. J Biomechanics. 29 : 1523-1529.

Léger L., Cloutier J., Rowan C.(1985) Testprogressive de course navette de 20 m.t avec paliers de une minute. Université de Montreal.

Léger L., Lambert J. (1982 b) A maximal multistage 20 m.t. shuttle run test to predict VO2 max . Eur. J. Appl. Physiol. 49: 1-12.

Léger L., Lambert J., Goulet A., Rowan C., Dinelle Y. (1984) Capacité aérobie des Québécois de 6 à 17 ans: Test navette de vingt métres avec paliers de une minute. Can. J. Appl. Sports. Sci. 9: 64-69.

Léger L., Rowan C., Asselin L., Cartier D., Massicotte D., Soulière D. (1982 a) Test progressive de course navette de vingt mètres de Leger. Fascicule B6. Test d’évaluation de la condition physique de l’adulte (TECPA), Kino-Québec.

Margaria R. (1938) Sulla fisiologia, e specialmente sul consumo energetico della marcia a varie velocità ed inclinazioni del terreno. Atti Ass. Naz. Lincei. 7 : 299-368.

Margaria R., Cerretelli P., Aghemo P., Sassi G (1963) Energy cost of running. J. Appl. Physiol. 18 : 367-370.

Mc Mahon T.A, Valiant G., FrederiK E.C. (1987) Groucho running. J. Appl. Physiol.. 62 : 2326-2337.

Mc Mahon T.A. (1984) Muscles, reflexes and locomotion. Princeton.

Mc Mahon T.A. (1990) Spring like properties of muscle and reflexexs in running. In: Winters J.M., Woo S.L. (eds) Multiple muscle systems: biomechanics and movement organisation. Springer-Verlag, pp 578-590.

Mc Mahon T.A., Cheng G.C. (1990) The mechanics of running: how does stiffness couple with speed? J. Biomechanics 23: 65-78.

Morgan D., Martin P., Craib M., Caruso C., Clifton R., Hopwell R.(1994) Effect of stride lenght optimization on the aerobic demend of running. J. Appl. Physiol.. 77: 245-251.

Saltin B., Åstrand P.O. (1967) Maximal oxigen uptake in athletes. J. Appl. Physiol. 23 : 353-358.

Shorten M.R. (1987) Muscle elasticity and human performance. Med. Sport Sci. 25 :1-18.

Svedenhag J., Sjödin B., (1994) Body-mass modified running economy and step lenght in elite male middle and long distance runners. Int J. Sports Med. 15: 305-310.

Taylor C.R. (1985) Force development during sustained locomotion: a determinant of gait, speed and metabolic power. Journal of Experimented Biology 115: 253-262.

Viale F., Dalleau G., Lacour J.R., Belli A. Foot orientation and leg stiffness. Foot & Ankle in corso di pubblicazione.

Williams K. (1985) Biomechanics of running. Exerc Sport Sci Rev. 13: 389-441