I parametri biomeccanici dello sprint
The biomechanical parameters in sprint
di Bisciotti GN^(1-3)., Necchi P⁽²⁾. Iodice GP⁽¹⁾., Sagnol JM⁽⁴⁾

SOMMARIO

Lo scopo del presente studio è stato quello di stabilire la relazione forza-velocità ed i vari aspetti della produzione di potenza durante uno sprint. Per questo scopo è stata utilizzata un’apparecchiatura che consentisse di aumentare le richieste di forza da parte dell’atleta durante uno sprint effettuato in condizioni di terreno. Nel presente studio sono stati considerati 10 atleti di sesso maschile praticanti calcio la cui età, peso ed altezza erano rispettivamente 25.7 ± 3 anni (media + deviazione standard), 75.9 ± 4.5 kg e 177.7 + 3.8 cm .

La relazione forza-velocità ottenuta è stata di tipo fortemente lineare (r²= 0.89 p< 0.001)

La potenza registrata nei vari tipi di sprint richiesti dal protocollo sperimentale è risultata essere compresa in un range di 399.89 ±51.58 e 679.27 ±128.43 W.

Le relazioni velocità-potenza e forza-potenza sono entrambe di tipo parabolico e presentavano rispettivamente un r² di 0.35 (p<0.001) e di 0.67 (p<0.001)

Vengono inoltre affrontate alcune problematiche di ordine metodologico riguardanti l’utilizzo nei programmi di allenamento degli sprint in salita.

the biomechanical parameters in sprint

The purpose of this study was to determine the force -velocity relationship and various aspects of power production during a sprint. To reach this aim, we used a device able to increase the force required by the athlete, during a sprint effected in field conditions. In the present study 10 male football players of national level were considered, whose age weight and height were respectively 25.7 ± 3 years (mean + standard deviation), 75.9 ± 4.5 kg. and 177.7 ± 3.8cm.

The force-velocity relationship obtained in this study was strongly linear (r²=0.89, p<0.001); the power required by the experimental protocol and recorded during the various sprints effected was included in a range between 399.89 ± 51.58 and 128.43 W.; both power- velocity and power- force relationships were parabolic and presented respectively a r² of 0.35 (p<0.001) and 0.67 (p<0.001).

Moreover, this study dealt with some methodological problems on the use of uphill sprints in the training programs..

INTRODUZIONE

La relazione che intercorre tra la forza sviluppata a differenti velocità di contrazione e la velocità di contrazione stessa, descrive una delle caratteristiche meccaniche fondamentali del muscolo scheletrico. I primi studi concernenti il rapporto tra la forza e la velocità di contrazione del muscolo scheletrico in vitro risalgono a Fenn e Marsh ¹ che riferirono una relazione esponenziale tra questi due parametri, ritrovata in seguito anche da Aubert ²ma già nel 1938 Hill ³, sempre su muscolo isolato, propose una relazione di tipo iperbolico. Tuttavia ultimamente, anche se alcuni Autori, considerando dei movimenti monoarticolari, hanno ritrovato nell’uomo, in condizioni di attivazione naturale, delle relazioni forza-velocità di tipo iperbolico od esponenziale ^4-5-6-7, molti altri riferiscono, in simili condizioni sperimentali concernenti movimenti pluriarticolari, una relazione di tipo lineare,^{8-9-10-11-12-13-14}. Un ulteriore dettaglio degno di nota sulla relazione forza-velocità, è quello riferito da alcuni Autori ^4-15-16 che riveriscono un livellamento della relazione forza-velocità stessa che si verificherebbe a basse velocità di contrazione. Tale fenomeno sarebbe spiegabile attraverso un meccanismo di regolazione nervosa che limiterebbe la produzione di forza nel momento in cui quest’ultima raggiunga determinati valori. Per ciò che riguarda la problematica specifica della relazione forza velocità durante la corsa, non si può fare a meno di notare come quest’ultima sia stata relativamente poco indagata, i dati a nostra conoscenza riguardano uno studio di Best e Partrige ¹⁷ effettuato su due soli soggetti e di Wandevalle e Gajer ¹⁸ effettuato su atleti di elite durante lo sprint. Mentre nel primo studio non poté essere tratta nessuna conclusione sulla relazione forza-velocità, nel secondo i due Autori proposero una correlazione di tipo lineare tra forza e velocità di corsa. Recentemente Jaskólska e coll.¹⁴ hanno proposto una relazione lineare tra forza e velocità di corsa effettuata su di uno speciale tread-mill sul quale il soggetto veniva vincolato ad un cavo sul quale un trasduttore di forza misurava la forza di trazione esercitata. Tuttavia tali condizioni esperimentali, che ritroviamo peraltro anche in altri protocolli per il calcolo della produzione di potenza durante lo sprint ^19-20, si allontanano sensibilmente, a nostro avviso, da quelle che sono le condizioni naturali di esecuzione del gesto normalmente osservabili su campo. Oltre alla relazione forza-velocità, anche la produzione di potenza costituisce un parametro largamente utilizzato per la determinazione delle caratteristiche muscolari dell’atleta. In effetti nell’ambito di gesti motori la cui esecuzione sia limitata da un punto di vista temporale, la produzione di potenza costituisce spesso la variabile che determina la prestazione stessa ¹⁴. La potenza meccanica prodotta da un gruppo muscolare dipende direttamente dalla forza e dalla velocità di contrazione ed il suo valore massimale sarà quindi il prodotto dei valori ottimali di forza e di velocità. Nell’ambito specifico dell’allenamento dello sprint, o di altre discipline che comunque ricerchino un aumento della velocità di percorrenza massimale sulle brevi distanze, come ad esempio il calcio, lo sprint in salita è una metodologia di allenamento largamente praticata ^21-22. Questo tipo di metodologia di allenamento trova la sua giustificazione nella ricerca di un aumento della potenza prodotta durante lo sprint stesso rispetto allo sprint effettuato in piano ^23-24-25, appare quindi chiaro l’interesse pratico costituito dal poter identificare la percentuale di pendenza alla quale l’atleta riesce ad esprimere la massima produzione di potenza. Lo scopo di questo lavoro è appunto quello di determinare la relazione forza-velocita e la produzione di potenza durante uno sprint effettuato nelle condizioni che meglio si avvicinano a quelle dell’esecuzione in situazione naturale. L’originalità di questo studio risiede nel fatto di utilizzare "su campo" una strumentazione che permetta l’aumento della forza di trazione da parte dell’atleta nell’effettuazione di uno sprint la cui esecuzione sia il più sovrapponibile possibile a quella naturale, unita al fatto di poter simulare, attraverso l’indice di frizione stesso, la meccanica dello sprint in salita effettuato su diverse percentuali di pendenza.

MATERIALI E METODI

Soggetti

Nel presente studio sono stati considerati 10 atleti di sesso maschile praticanti calcio la cui età, peso ed altezza erano rispettivamente 25.7 ± 3 anni (media ± deviazione standard), 75.9 ± 4.5 kg e 177.7 ± 3.8 cm .

Tutti i soggetti hanno mantenuto nel periodo del test la loro normale attività d’allenamento, consistente in 4 sedute settimanali della durata media di 2 ore e nessuno di loro presentava patologie di tipo dermatologico, muscolare o neuromuscolare. Inoltre, tutti gli atleti che hanno preso parte al protocollo di test, erano stati preventivamente informati sullo scopo della ricerca e sui possibili rischi ad essa connessi.

Protocollo

Ad ogni soggetto è stato richiesto di effettuare una serie di sprint della lunghezza di 30 m. utilizzando una speciale apparecchiatura (figura.1) costituita da un rullo a frizione regolabile al quale l’atleta veniva vincolato tramite un cavo ed una cintura posta a livello del bacino. In tale apparecchiatura l’indice di frizione era controllato attraverso un dinamometro digitale a cella di carico (Mod. Ergo Meter, Globus Italia, Codogné, Italy. Sample rate 100 Hz, non-linearity histeresis and repeatability 0.002 of RO, temperature compensated 0° to 50°, charge scale 0-300 kg)

Allo scopo di richiedere un crescente impegno di forza durante la serie di sprint richiesti,la frizione, imposta agli atleti durante gli sprint stessi, era scelta in modo tale da simulare il lavoro richiesto durante l’esecuzione di un sprint della stessa lunghezza ma effettuato su di una pendenza di vario grado.

Il protocollo sperimentale prevedeva che ogni soggetto eseguisse

L’indice di frizione ( trascurando il peso del cavo) veniva calcolato attraverso la seguente formula:

Fa = P · tang b ²⁶

Nella quale Fa è l’indice di attrito della frizione, P il peso del soggetto, tang b la tangente dell’angolo relativo alla salita che si intende simulare.

Ogni prova veniva cronometrata con l’ausilio di un sistema di fotocellule di sensibilità pari al millesimo di secondo (Ergo Timer, Globus Italia, Codogné, Italy).

La potenza media espressa durante l’azione di sprint in condizioni naturali veniva calcolata attraverso la seguente formula.

P= (0.5 M · V2) · t-1 [ W ]

Nella quale M è uguale alla massa (kg) del soggetto, V la velocità di percorrenza (m · s-1) e t il tempo di percorrenza (s).

La potenza media espressa durante l’azione di sprint nel caso di simulazione di sprint in pendenza, simulata veniva calcolata attraverso la seguente formula.

P= [ 0.5 M · V2 + (F · d) ] · t-1 [ W ]

Nella quale M è uguale alla massa (kg) del soggetto, V la velocità di percorrenza (m · s-1), F l’indice di frizione (N) applicato all’apparecchiatura alla quale il soggetto era vincolato per simulare la percentuale di pendenza desiderata, d la distanza percorsa durante lo sprint (m) e t il tempo di percorrenza (s).

Statistica

Per ogni variabile considerata sono stati calcolati gli indici statistici ordinari come media, varianza e deviazione standard. La differenza delle medie dei valori di potenza registrati durante i test di sprint sono stati verificati attraverso un test non parametrico di Wilkoxon. La relazione forza-velocità e stata calcolata effettuando una regressione lineare semplice tra i valori dell’indice di frizione e la velocità di percorrenza registrati durante le prove di sprint.

I valori di forza e potenza e di forza e velocità sono stati tra loro correlati attraverso una relazione polinomiale di secondo grado.

I valori di potenza media registrati durante i test S 0%, S 5%, S 10%, S 15%, S 20%, S 25% ed S 30% sono stati tra loro correlati attraverso un tes di correlazione dei ranghi di Spearman.

La significatività statistica è stata posta a p<0.05.

RISULTATI

La relazione forza-velocità ottenuta è di tipo fortemente lineare (r²= 0.89 p< 0.001) (Grafico 1)

Le relazioni velocità-potenza e forza-potenza sono entrambe di tipo parabolico e presentano rispettivamente un r² di 0.35 (p<0.001) e di 0.67 (p<0.001)

La relazione tra la percentuale di salita simulata durante le prove di sprint e la potenza prodotta è anch’essa ben descritta da una curva polinomiale di secondo grado (r2 =0.89 p<0.001) (Grafico 2).

I valori di potenza registrati durante i test S 0%, S 5%, S 10%, S 15%, S 20%, S 25% ed S 30% sono riportati in tabella 1.

I risultati del test di correlazione dei ranghi di Spearman effettuato utilizzando i valori di potenza media registrati durante i test S 0%, S 5%, S 10%, S 15%, S 20%, S 25% ed S 30%, sono presentati in tabella 2.

DISCUSSIONE

La relazione forza-velocità registrata nel presente studio si è rivelata di tipo fortemente lineare (r²= 0.89, p< 0.001). Questo risultato avvallerebbe l’ipotesi, non confermata sperimentalmente a causa dell’esiguità dei soggetti considerati, già avanzata da Best e Partrige ¹⁷ed in seguito riproposta da Vandewalle e Gajer ¹⁸. Tuttavia ci preme sottolineare come l’originalità di questo studio risieda nel fatto di avere ottenuto una relazione forza-velocità nello sprint in condizioni di terreno, questo dato, a nostra conoscenza, non trova altri riscontri nell’ambito dell’attuale bibliografia.

Questa linearità della relazione forza-velocità ritrovata durante lo sprint è in accordo con quanto ritrovato da numerosi Autori in altri protocolli sperimentali, che comprendevano: il movimento di pedalata su bicicletta, su bicicletta isocinetica e lo sprint su treadmill ^{9-10-11-12-13-14}. La linearità della relazione forza-velocità ritrovabile nella corsa, come d’altro canto durante la pedalata, è probabilmante da ricondursi al fatto che entrambi questi tipi di movimento sono il risultato di un’azione sinergica di numerosi gruppi muscolari che agiscono su di un numero limitato di articolazioni ¹⁴. In situazione di attivazione naturale infatti le proprietà meccaniche del muscolo si esprimono attraverso l’architettura muscolo-scheletrica e secondo un livello di attivazione che dipende dal sistema di comando centrale. Inoltre occorre considerare che il muscolo in situ rappresenta un sistema asservito, il cui segnale di uscita (output) dipende il larga parte dalle caratteristiche del segnale d’entrata (input) ²⁷. Un altro importante fattore da considerare nel momento in cui si intendesse paragonare il comportamento muscolare in vivo a quello riscontrabile in vitro, è costituito dal fatto che in situ la relazione forza-velocità riflette il comportamanto dell’insieme dei muscoli attivi, quindi sia degli agonisti che degli antagonisti, e che inoltre la forza di ciascun gruppo muscolare sollecitato dipende dal proprio livello di attivazione ²⁸, tale situazione appare ovviamente molto lontana da quanto invece sta alla base della relazione forza-velocità su muscolo isolato. Un ultimo ed ulteriore fattore da considerare per poter spiegare la differenza tra la linearità della relazione forza-velocità ritrovabile nel corso di un movimento naturale, e quella iperbolica ritrovata in sperimentazioni effettuate su muscolo isolato, riguarda la deformazione degli elementi elastici in serie, la pennazione delle fibre muscolari, nonchéil rapporto dei bracci di leva riscontrabili durante il movimento naturale stesso, nonchè la pennazione delle fibre muscolari ¹⁸.

Nel corso di un movimento naturale che preveda una fase eccentrica immediatamente seguita da una contrazione concentrica,situazione normalmente definita con il termine di "ciclo stiramento-accorciamento", si verifica, nel corso della fase eccentrica stessa, un accumulo di energia elastica potenziale a livello della Componente Elastica Seriale (SEC), che è a sua volta anatomicamente identificabile a livello del tendine, del collagene intramuscolare e della stria Z, per ciò che riguarda la sua parte passiva ed a livello della porzione S₂ della miosina, per quello che concerne la sua parte attiva ^29-30. L’energia elastica potenziale accumulata durante la fase eccentrica viene restituita sotto forma di lavoro meccanico nella successiva fase concentrica, questo determina una modificazione ed uno spostamento a destra e verso l’alto della relazione forza-velocità in vivo, rispetto a quanto non avvenga nel muscolo isolato ³¹.

Anche la struttura muscolare è in grado d’influenzare la relazione forza-velocità, la disposizione delle fibre muscolari infatti è raramente parallela alla lunghezza del muscolo ma si presenta piuttosto in un rapporto obliquo rispetto all’asse longitudinale del muscolo stesso secondo un angolo denominato "angolo di pennazione" ³². La forza massimale di un muscolo pennato risulta superiore a quella esercitabile da un muscolo a fibre parallele mentre al contrario la pennazione di un muscolo diminuisce la sua massima velocità di accorciamento ³³.

Per ciò che riguarda il rapporto dei bracci di leva, occorre considerare che, siccome il momento di una forza risulta uguale al prodotto tra il braccio di leva ed il valore della forza stessa, si ottiene la seguente uguaglianza:

F_M . h = F_P .H

da cui:

F_P = F_Mh / H

Nelle quali h rappresenta il braccio di leva della forza F_M del muscolo in rapporto al centro articolare ed H è il braccio di leva della forza F_P che viene esercitata a livello esterno sul punto P.

Di conseguenza la forza che viene esercitata a livello esterno dipende dal rapporto intercorrente tra i bracci di leva h ed H. Contestualmente anche la velocità V_P di spostamento del punto P, determinata dall’accorciamento muscolare, M risulterà uguale a:

V_P = V_M . H / h

Nella quale V_M rappresenta la velocità di accorciamento del muscolo M.

Da questo consegue che nel corso di un movimento articolare i valori di forza massimale isometrica (F₀) e di velocità corrispondente a forza nulla (V₀), dipendano non solamente dalle proprietà contrattili del muscolo e dall’angolo di pennazione delle fibre muscolari che lo compongono ma anche dal rapporto h / H dei bracci di leva delle forze M e P ³³.

Per tutta questa serie di motivi non è pensabile potersi attendere che il comportamento meccanico del muscolo in situ possa essere adeguatamente descritto dalle semplici relazioni meccaniche ottenute dalle sperimentazioni effettuate sul muscolo isolato ^8-18. La relazione forza-velocità rimane comunque un interessante metodo di monitorizzazione degli effetti dell’allenamento ^12-33, ed in particolare la metodica di costruzione della suddetta relazione presentata nell’ambito di questo studio, potrebbe fornire delle interessanti informazioni nell’ambito dell’allenamento dello sprint. Attraverso la costruzione della relazione forza-velocità infatti è possibile estrapolare due importanti parametri biomeccanici relativi al comportamento muscolare in vivo. Il primo è costituito dal valore F₀ che rappresenta la massima capacità contrattile del gruppo muscolare considerato ³⁴ ed il secondo dal valore V₀, che oltre a fornire informazioni sulla massima velocità contrattile del muscolo ³⁴, può suggerire importanti informazioni per ciò che riguarda la tipologia e l’architettura muscolare del soggetto. Un valore di V₀ elevato infatti potrebbe suggerire una predominanza di fibre muscolari rapide; tuttavia dal momento che occorre considerere anche il ruolo ricoperto dalla lunghezza dei bracci di leva e dall’angolo di pennazione, é più corretto formulare l’ipotesi che un valore elevato di V₀ possa essere determinato da una predominanza di fibre rapide e/o da bracci di leva corti e/o da un’architettura muscolare particolarmente favorevole, come ad esempio nel caso di fibre muscolari lunghe che presentino un limitato angolo di pennazione.

Inoltre i dati desunti dal presente studio non permettono di confermare l’ipotesi di un livellamento della relazione forza-velocità a basse velocità di contrazione già avanzata da altri Autori ^4-15-16, questo confermerebbe i dati ritrovabili in proposito, sia in altri lavori sperimentali concernenti la relazione forza-velocità durante la corsa ¹⁴, che in altri studi che escluderebbero l’apparizione di un plateau nella relazione coppia di forza-velocità durante movimenti isocinetici effettuati a basse velocità angolari ^35-36.

Un ulteriore aspetto degno di una certa attenzione che scaturisce dai dati raccolti, è rappresentato dal fatto di come il test S 0% sia correlato positivamente solamente con i test S 5% ed S 10% (rispettivamente r² = 0.94, p< 0.001 ed r2=0.68, p< 0.05) ma non con gli altri test di sprint.

Questo potrebbe testimoniare il cambiamento biomeccanico della corsa che si viene a stabilire nel momento in cui l’incremento della forza richiesta durante lo sprint stesso superi un determinato limite.

Anche i valori di potenza media registrati nei test di sprint (range: 399.89 ± 51.58 — 679 ± 128.43 W) risultano in linea con quanto riportato da altri Autori, i quali riferiscono valori medi di potenza registrati durante uno sprint compresi in un range di 488 ± 254 e 717 ± 200 W ¹⁴e di 606 ± 134 e 681 ± 134 watt ³⁷.

Le relazioni velocità-potenza e forza-potenza registrate sono entrambe descritte da una relazione di tipo parabolico e presentano rispettivamente un r² di 0.35 (p<0.001) e di 0.67 (p<0.001).

La produzione di potenza quindi, durante l’esecuzione di uno sprint effettuato contro una resistenza esterna, come nel presente studio, sarebbe maggiormente dipendente dalla produzione di forza richiesta che dalla velocità raggiungibile.

A questo proposito è interessante notare come la relazione esistente tra la percentuale di salita simulata durante le prove di sprint e la potenza prodotta sia ben descritta da una curva polinomiale di secondo grado (r² =0.89 p<0.001).Il picco di produzione di potenza si otterrebbe con uno sprint effettuato su di una salita di pendenza pari al 26.24 %. Dal momento che gli sprint effettuati su salite, in situazione reale di allenamento, sono una metodologia di lavoro molto utilizzata in numerose attività sportive, come l’atletica leggera, la pallavolo od il football ^31-38-39, questo dato dovrebbe essere tenuto in forte considerazione da parte dei tecnici delle varie discipline nella stesura dei programmi di allenamento.

In conclusione questo lavoro, non solo ha permesso di sottolineare un aspetto teorico originale, quale la determinazione della relazione forza-velocità durante uno sprint effettuato in condizioni di terreno ma anche di poter trarre delle indicazioni di ordine pratico, atte all’ottimizzazione della produzione di potenza, nell’ambito di metodologie di allenamento, come lo sprint in salita, già universalmente adottate nell’ambito di numerose discipline sportive ma sinora prive di riferimenti sperimentali.

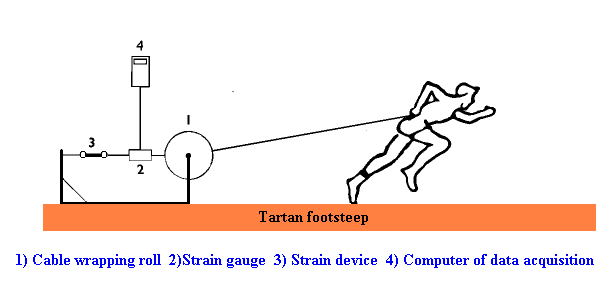
Figure 1: the device used during the test

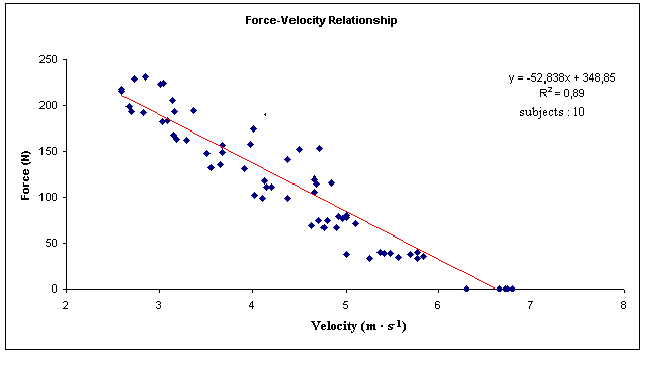
Table 5: Force-velocity relationship

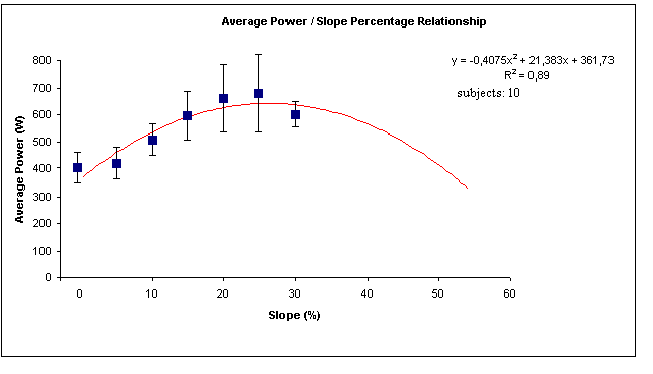
Table 6: Average power-slope percentage relationship

Tabella 1: valori di potenza media registrati durante i diversi tipi di test di sprint.

Tabella 2: matrice di correlazione dei ranghi di Spearman concernente i valori di potenza media registrati durante i diversi tipi di test di sprint..

* p<0.05 ** p<0.01 *** p<0.001

Bibliografia